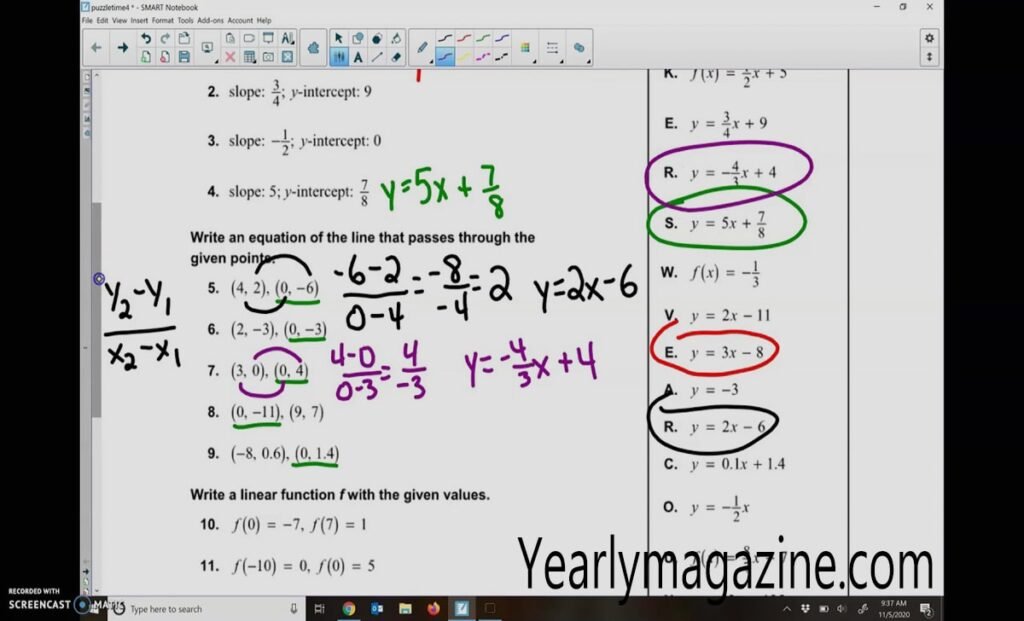
Introduction
Finding yourself stuck on the 7.4 puzzle time answer key problems? You’re not alone. These mathematical puzzles can be challenging, but with the right approach and understanding, they become much more manageable. This comprehensive guide provides detailed solutions to all 7.4 Puzzle Time questions, along with explanations that will help you master the underlying concepts.
Whether you’re a student working through homework assignments or someone looking to strengthen your problem-solving skills, this answer key will serve as your roadmap to success. We’ll walk through each solution step-by-step, highlight common pitfalls, and share proven strategies that make these puzzles easier to tackle.
By the end of this guide, you’ll not only have the answers you need but also the confidence to approach similar problems independently.
Understanding 7.4 Puzzle Time: Key Mathematical Concepts
The 7.4 puzzle time answer key section typically focuses on algebraic expressions, equation solving, and mathematical reasoning. These puzzles are designed to test your ability to apply multiple mathematical concepts simultaneously while thinking critically about problem-solving approaches.
Most 7.4 puzzles incorporate several core areas:
Algebraic Manipulation: Working with variables, coefficients, and mathematical operations to simplify expressions or solve for unknown values.
Pattern Recognition: Identifying sequences, relationships, and recurring themes within numerical or algebraic structures.
Logical Reasoning: Using deductive and inductive thinking to arrive at solutions through systematic analysis.
Multi-Step Problem Solving: Breaking down complex problems into manageable components that can be solved sequentially.
Understanding these foundational elements is crucial because 7.4 puzzles rarely test just one skill in isolation. Instead, they require you to synthesize multiple mathematical concepts to reach the correct answer.
Step-by-Step Solutions to 7.4 Puzzle Time Questions
Problem Type 1: Algebraic Expression Puzzles
These problems typically present you with an algebraic expression that needs to be simplified or evaluated. The key is to follow the order of operations while carefully tracking positive and negative signs.
Start by identifying like terms and grouping them together. Next, perform any multiplication or division operations. Finally, combine like terms by adding or subtracting coefficients.
When working with variables, remember that you can only combine terms with identical variable parts. For example, 3x and 5x can be combined to make 8x, but 3x and 5y cannot be simplified further.
Problem Type 2: Equation Solving Challenges
Equation-based puzzles require you to find the value of unknown variables. Begin by isolating the variable on one side of the equation using inverse operations.
If you have addition on one side, use subtraction to cancel it out. If you have multiplication, use division. Remember that whatever operation you perform on one side of the equation must also be performed on the other side to maintain balance.
For multi-step equations, work systematically from the outside in. Handle parentheses first, then deal with multiplication or division, and finally address addition or subtraction.
Problem Type 3: Word Problem Applications
Word problems in the 7.4 section often require you to translate verbal descriptions into mathematical expressions or equations. Read the problem carefully and identify what information is given and what you need to find.
Look for key phrases that indicate mathematical operations. Words like “sum,” “total,” and “combined” suggest addition. Terms such as “difference,” “less than,” and “decreased by” indicate subtraction.
Once you’ve translated the problem into mathematical language, solve using the appropriate techniques for the type of equation or expression you’ve created.
Visual Problem-Solving Strategies
Many students find success by creating visual representations of 7.4 puzzle problems. Drawing diagrams, making tables, or sketching graphs can help clarify relationships between different elements of a problem.
For algebraic expressions, consider using color coding to identify like terms. This visual approach reduces errors when combining terms and makes the simplification process more systematic.
When dealing with word problems, try creating a simple diagram that shows the relationships described in the problem. This technique is particularly helpful for problems involving distances, rates, or geometric relationships.
Tables are excellent tools for organizing information in multi-step problems. Create columns for known values, unknown values, and intermediate calculations to keep your work organized and reduce computational errors.
Proven Tips for Puzzle Success
Read Twice, Solve Once: Always read each problem at least twice before beginning your solution. This helps ensure you understand what’s being asked and prevents careless mistakes.
Show Your Work: Even when using this answer key, practice writing out each step of your solution. This builds muscle memory and helps you identify where errors might occur.
Check Your Answers: Substitute your solution back into the original problem to verify it’s correct. This is especially important for equation-solving problems.
Practice Estimation: Before diving into detailed calculations, estimate what a reasonable answer might look like. This helps you catch major errors in your problem-solving approach.
Use Systematic Approaches: Develop consistent methods for approaching each type of problem. Having a reliable process reduces the likelihood of skipping important steps.
Common Mistakes to Avoid
One of the most frequent errors students make is rushing through the problem without fully understanding what’s being asked. Take time to identify the specific question before beginning your calculations.
Sign errors are another common pitfall. When working with negative numbers or subtracting expressions, double-check your positive and negative signs at each step. A single sign error can throw off your entire solution.
Many students also struggle with the order of operations. Remember PEMDAS (Parentheses, Exponents, Multiplication and Division from left to right, Addition and Subtraction from left to right) and apply it consistently.
When solving equations, be careful not to perform different operations on each side of the equation. Whatever you do to one side must be done to the other to maintain equality.
Finally, avoid the temptation to skip steps in your written work. Even if you can do some calculations mentally, writing out each step helps prevent errors and makes it easier to identify mistakes if your answer is incorrect.
Additional Practice Resources
Mastering 7.4 puzzles requires consistent practice beyond just reviewing answer keys. Consider working through similar problems from your textbook or online resources to build your problem-solving skills.
Many educational websites offer interactive algebra practice problems that provide immediate feedback. This can be particularly helpful for identifying specific areas where you need additional practice.
Study groups can also be valuable for tackling challenging puzzles. Explaining your solution process to others helps reinforce your understanding, while listening to different approaches can expand your problem-solving toolkit.
If you’re struggling with particular types of problems, consider seeking help from your teacher, tutor, or online educational platforms that offer personalized instruction.
Frequently Asked Questions
What should I do if my answer doesn’t match the answer key?
First, carefully review each step of your solution to identify where the error occurred. Check your arithmetic, sign handling, and application of mathematical rules. If you still can’t find the mistake, try solving the problem using a different approach.
How can I improve my speed when solving these puzzles?
Speed comes with practice and familiarity. Focus first on accuracy and understanding the concepts thoroughly. As you become more comfortable with the problem types, your speed will naturally increase.
Are there any shortcuts for solving 7.4 puzzles?
While there are some pattern recognition techniques that can speed up your work, it’s important to master the fundamental approaches first. Shortcuts are most effective when you have a solid understanding of the underlying mathematics.
What if I understand the answer key but can’t solve similar problems on my own?
This suggests you may be memorizing solutions rather than understanding the process. Try covering up the answer key and working through problems step-by-step, only checking your work when you’re finished.
Mastering Mathematical Problem-Solving
Success with 7.4 Puzzle Time problems extends far beyond memorizing answer keys. The real value lies in developing systematic problem-solving skills that will serve you throughout your mathematical education.
Focus on understanding the reasoning behind each solution rather than simply copying answers. Practice regularly with similar problems to build confidence and fluency. Most importantly, don’t be discouraged by initial difficulties—mathematical problem-solving is a skill that improves significantly with deliberate practice.
Remember that these puzzles are designed to challenge your thinking and help you grow as a mathematical problem-solver. Use this answer key as a learning tool, not just a source of quick answers, and you’ll find yourself becoming more confident and capable with each practice session.